💾 Parte 1 — As Raízes Antigas

tecnologia

história da computação

computação

história

instrumentos de cálculo

antiguidade

ábaco

Anticítera

cálculo

lógica

civilizações antigas

Do ábaco à Máquina de Anticítera — os primeiros instrumentos que transformaram o pensamento em cálculo.

Autor

Blog do Marcellini

Data de Publicação

13 de outubro de 2025

← História da Computação · ← Início

Ilustração simbólica da evolução dos computadores

1 💾 Parte 1 — As Raízes Antigas

“Antes dos circuitos, vieram as ideias.
Antes do silício, o cálculo era humano.”

1.1 🏺 O impulso de contar

A história da computação começa muito antes da eletricidade, dos circuitos e dos códigos binários.
Ela nasce no instante em que o ser humano descobre o poder do símbolo — a capacidade de fazer o mundo caber em um sinal, um traço, uma pedra.

Esse impulso de representar o real por meio de abstrações é a semente tanto da matemática quanto da computação.
Marcas feitas em ossos, pedras ou argila tornaram-se extensões da mente, permitindo que o pensamento se fixasse fora do corpo, transformando memória em matéria.

Entre os exemplos mais antigos está o Osso de Ishango, datado de cerca de 20 mil anos atrás e encontrado nas margens do Lago Eduardo, na África Central.
Em seu pequeno corpo de marfim fossilizado, veem-se colunas de entalhes agrupados — talvez contagens lunares, talvez operações aritméticas primitivas.
O que importa é o salto cognitivo: ali surge a ideia de registro, o ato de gravar um raciocínio no mundo físico.

“Contar é o primeiro algoritmo.
O resto é apenas sua automatização.”

🪶 Curiosidade Arqueológica — Os Primeiros Registros Numéricos

Osso de Lebombo (Suazilândia, ~35 000 a.C.) — entalhes regulares para contagem simples.
Tally sticks europeus — bastões de madeira com cortes que registravam trocas comerciais.
Tábuas de argila mesopotâmicas — controle de grãos e impostos: os primeiros bancos de dados da humanidade.

📦 Do token ao texto — contar antes de escrever

Muito antes da escrita cuneiforme, o Crescente Fértil usava fichas de argila (tokens) para registrar bens (grãos, rebanhos). Ao longo de milênios, esses tokens evoluíram para marcas em tábuas e, por fim, para a escrita — um arco em que contar/registrar precede escrever. É a proto-história dos nossos bancos de dados.

1.2 🦴 Osso de Ishango (c. 20 000 a.C.)

O Osso de Ishango, descoberto em 1950 pelo arqueólogo Jean de Heinzelin de Braucourt, apresenta três colunas de entalhes verticais agrupados em padrões numéricos não aleatórios.
Pesquisas evidenciam regularidade matemática, com agrupamentos e possíveis dobramentos (2×); alguns autores sugerem relações com base 12. Há propostas de que certas sequências remetam a números primos entre 10 e 20, mas essa leitura é disputada. O consenso prudente: tratava-se de um instrumento de contagem/registro, não prova direta de teoria de primos.

O artefato mostra o raciocínio matemático materializado em um objeto físico.
Guardado no Real Instituto de Ciências Naturais da Bélgica, simboliza o nascimento da consciência numérica.

💡 Curiosidade e legado

O Osso de Ishango é frequentemente citado como um dos primeiros artefatos matemáticos e, simbolicamente, um “dispositivo de armazenamento de dados” humano.

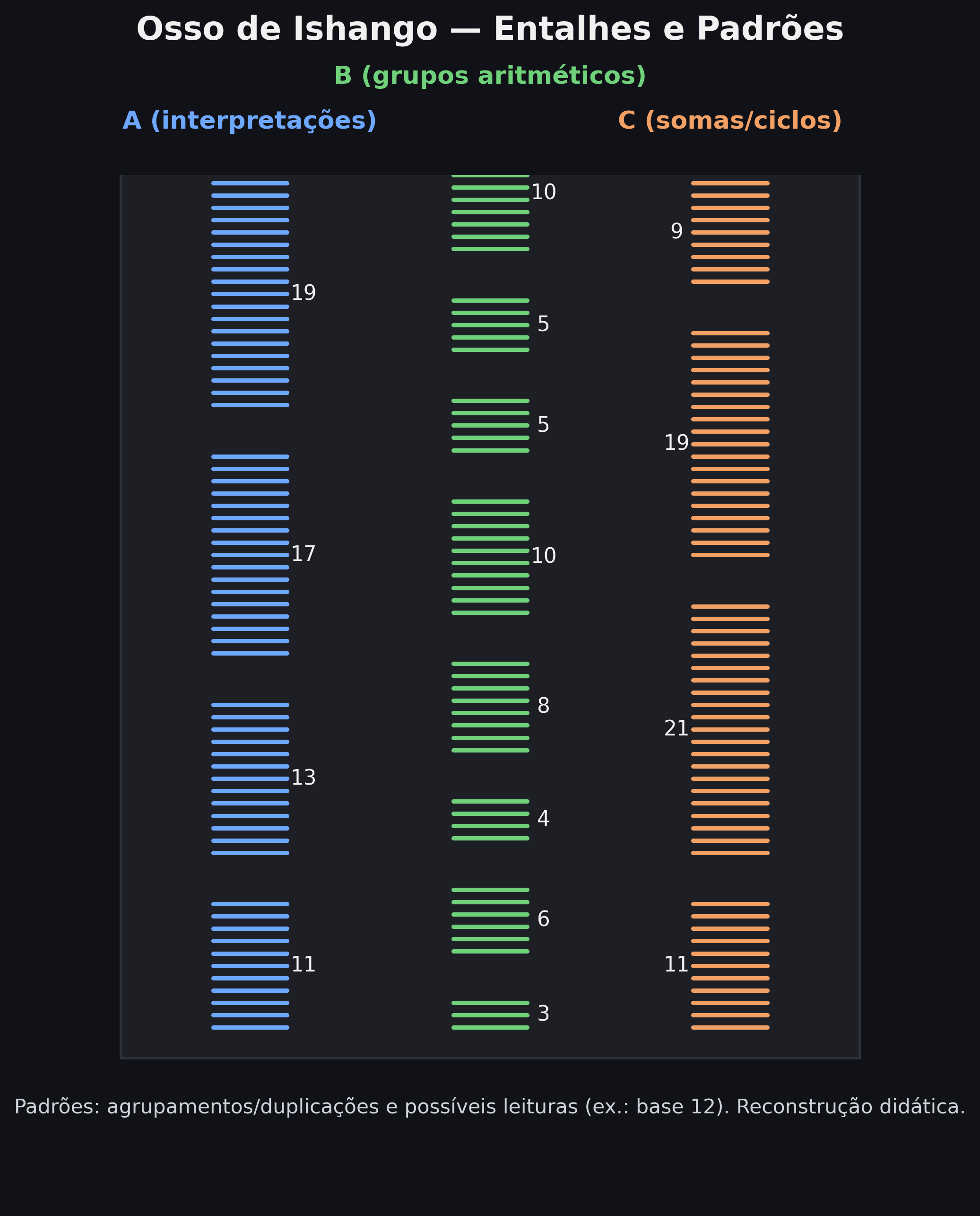
Diagrama didático das três colunas do Osso de Ishango

Clique para ver o código (Python) — Diagrama das Três Colunas

# Gera: images/ishango-diagrama-colunas.png e .svg

import os
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from matplotlib.collections import LineCollection

col_A = [11, 13, 17, 19]
col_B = [3, 6, 4, 8, 10, 5, 5, 10]
col_C = [11, 21, 19, 9]

os.makedirs("images", exist_ok=True)
bg, fg, subtle = "#111217", "#f1f1f1", "#cfd2d8"
col_colors = ["#6ea8fe", "#6fd17a", "#f3a065"]

fig, ax = plt.subplots(figsize=(8.4, 9.4), dpi=300)
ax.set_facecolor(bg); fig.patch.set_facecolor(bg)

x_positions = [0.24, 0.50, 0.76]
notch_len, dy_notch, dy_group, line_w = 0.08, 0.012, 0.038, 2.2

def draw_column(x, groups, color, label, y0=0.17, annotate_side="auto"):
    y = y0
    segs, centers = [], []
    side = -1
    for g in groups:
        for i in range(g):
            yi = y + i*dy_notch
            segs.append(((x - notch_len/2, yi), (x + notch_len/2, yi)))
        cy = y + (g-1)*dy_notch/2 if g>1 else y
        centers.append((cy, g))
        y += g*dy_notch + dy_group
    y_max = y - dy_group + dy_notch
    ax.add_collection(LineCollection(segs, colors=color, linewidths=line_w, capstyle="round"))
    ax.text(x, y_max + 0.024, label, ha="center", va="bottom", fontsize=12.5, weight="bold", color=color)
    for cy, g in centers:
        if annotate_side == "left":  side = -1
        elif annotate_side == "right": side = +1
        else: side *= -1
        ax.text(x + side*0.058, cy, str(g), ha="center", va="center", fontsize=10.5, color=fg)
    return y0, y_max

a_min, a_max = draw_column(x_positions[0], col_A, col_colors[0], "A (interpretações)", annotate_side="right")
b_min, b_max = draw_column(x_positions[1], col_B, col_colors[1], "B (grupos aritméticos)", annotate_side="right")
c_min, c_max = draw_column(x_positions[2], col_C, col_colors[2], "C (somas/ciclos)", annotate_side="left")

y_min, y_max = min(a_min,b_min,c_min), max(a_max,b_max,c_max)
ax.add_patch(Rectangle((0.10, y_min - 0.030), 0.80, (y_max - y_min) + 0.060,
                       facecolor="#1d1f25", edgecolor="#2c313a", lw=1.2, zorder=-5))

ax.text(0.5, y_max + 0.065, "Osso de Ishango — Entalhes e Padrões",
        ha="center", va="bottom", fontsize=16.5, color=fg, weight="bold")
ax.text(0.5, y_min - 0.068,
        "Padrões: agrupamentos/duplicações e possíveis leituras (ex.: base 12). Reconstrução didática.",
        ha="center", va="top", fontsize=10.2, color=subtle)

ax.set_xlim(0,1); ax.set_ylim(0,1); ax.axis("off")

plt.savefig("images/ishango-diagrama-colunas.png", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.savefig("images/ishango-diagrama-colunas.svg", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.close()

Nota

Leitura do diagrama. As três colunas mostram regularidade (agrupamentos e possíveis dobramentos). Leituras variam; evite certezas excessivas.

1.3 🧮 Do Ábaco às Tábuas

Antes das máquinas, vieram os instrumentos manuais — artefatos que tornaram o raciocínio visível e tangível.
Eles permitiram que a mente humana se projetasse no mundo, transformando pensar em gesto.

Ábaco sumério (c. 2400 a.C.) — pedrinhas em sulcos representando valores posicionais.
Ábaco chinês (suanpan, c. 500 a.C.) — contas móveis para operações complexas.
Tábuas de cálculo — registros de transações e somas.

💡 Ideia-chave

Esses dispositivos inauguram a interface homem-máquina: o cálculo mental ganhou forma física.

1.4 0️⃣ O golpe de gênio: notação posicional e o zero

Muito do que chamamos “computação” só decola quando números ganham posições e o zero vira número com regras próprias. Na Índia clássica, Brahmagupta (628) formaliza regras com zero e negativos; séculos depois, al-Khwārizmī difunde essa notação indo-arábica no mundo islâmico e, via traduções latinas, para a Europa — de onde nasce até a palavra algoritmo (Algoritmi de numero Indorum).

1.5 🧮 Ábaco Sumério (c. 2400 a.C.)

Clique para ver o código (Python) — Diagrama do Ábaco Sumério

# Gera: images/abaco-sumerio-diagrama.png e .svg

import os
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle, Circle

os.makedirs("images", exist_ok=True)

bg        = "#111217"
clay      = "#d8c2a8"
clay_edge = "#b79e86"
groove    = "#9d7f66"
stone     = "#6b4f3a"
stone_hi  = "#f0e6dc"
fg_global = "#f1f1f1"

fig, ax = plt.subplots(figsize=(8.6, 5.4), dpi=300)
ax.set_facecolor(bg); fig.patch.set_facecolor(bg)

rows = 5
cols = 8
spacing_y = 0.13
spacing_x = 0.095
x0, y0    = 0.17, 0.22

tablet_x, tablet_y = 0.10, 0.14
tablet_w, tablet_h = 0.80, 0.72
ax.add_patch(Rectangle((tablet_x, tablet_y), tablet_w, tablet_h,
                       facecolor=clay, edgecolor=clay_edge, lw=2.2, zorder=-5))

for i in range(rows):
    y = y0 + i * spacing_y
    ax.plot([x0, x0 + (cols-1)*spacing_x], [y, y],
            color=groove, lw=6, alpha=0.9, solid_capstyle="round")

positions = [(1,0), (2,0), (4,0),
             (0,1), (3,1), (6,1),
             (1,2), (5,2),
             (2,3), (5,3),
             (4,4), (6,4)]
for (cx, cy) in positions:
    x = x0 + cx*spacing_x
    y = y0 + cy*spacing_y
    r = 0.016
    circ = Circle((x, y), r, facecolor=stone, edgecolor="#3f2f24", lw=0.6)
    ax.add_patch(circ)
    ax.add_patch(Circle((x-0.005, y+0.004), r*0.45, facecolor=stone_hi, edgecolor="none", alpha=0.35))

for i in range(rows):
    y = y0 + i * spacing_y
    ax.text(tablet_x - 0.04, y, f"Ordem {i+1}",
            va="center", ha="right", color=fg_global, fontsize=10.5, fontweight="bold")

ax.text(0.5, tablet_y + tablet_h + 0.06,
        "Ábaco Sumério — Disposição dos Cálculos em Tábuas de Argila",
        ha="center", va="bottom", color=fg_global, fontsize=15, weight="bold")

ax.text(0.5, tablet_y - 0.04,
        "Linhas = ordens; círculos = cálculos móveis (pedrinhas).",
        ha="center", va="top", color="#cfd2d8", fontsize=10.5)

ax.set_xlim(0,1); ax.set_ylim(0,1); ax.axis("off")

plt.savefig("images/abaco-sumerio-diagrama.png", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.savefig("images/abaco-sumerio-diagrama.svg", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.close()

Nota

Como ler. Cada linha horizontal é uma ordem (unidades, dezenas…); mover pedrinhas entre linhas altera o valor.

1.6 🪨 Tábua de Salamina (c. 300 a.C.)

Um counting board grego de mármore (um abax), usado com pedrinhas móveis para cálculo posicional — ponte entre sulcos/pedrinhas e os ábacos com contas.
Peça no Museu Epigráfico de Atenas.

1.7 🧮 Ábaco Chinês (Suanpan, c. 500 a.C.)

Diagrama didático de um suanpan (ábaco chinês) com configuração 2:5

Clique para ver o código (Python) — Diagrama do Suanpan (2:5)

# Gera: images/linha-do-tempo-raizes-computacao-vertical.png e .svg

import os
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
from matplotlib.lines import Line2D

items = [
    ("Osso de Ishango", "c. 20 000 a.C.", "L"),
    ("Ábaco Sumério", "c. 2400 a.C.", "R"),
    ("Ábaco Chinês (Suanpan)", "c. 500 a.C.", "L"),
    ("Máquina de Anticítera", "c. 100 a.C.", "R"),
    ("Bastões de Napier", "1617", "L"),
    ("Régua de Cálculo", "1632", "R"),
    ("Máquina de Pascal", "1642", "L"),
]

os.makedirs("images", exist_ok=True)

bg = "#121316"
timeline_color = "#6ea8fe"
label_color = "#f1f1f1"
node_colors = ["#8b8dfb", "#75a7ff", "#57c0b6", "#6fd17a", "#e8c06f", "#f3a065", "#f17a54"]

fig = plt.figure(figsize=(8, 15.5), dpi=300)
ax = plt.gca()
ax.set_facecolor(bg); fig.patch.set_facecolor(bg)

x_center = 0.5
y_top, y_bot = 0.92, 0.10
n = len(items)
ys = [y_top - i * ((y_top - y_bot)/(n-1)) for i in range(n)]

ax.add_line(Line2D([x_center, x_center], [y_bot, y_top], lw=6, color=timeline_color, alpha=0.9, solid_capstyle="round"))
ax.text(0.5, 0.965, "Raízes da Computação", ha="center", va="center", fontsize=24, color=label_color, weight="bold")

for i, ((label, date, side), y) in enumerate(zip(items, ys)):
    ax.add_patch(Circle((x_center, y), 0.008, color=node_colors[i], ec="none"))
    if side == "L":
        x_text = x_center - 0.02; ha = "right"; x_tick = x_center - 0.015
    else:
        x_text = x_center + 0.02; ha = "left";  x_tick = x_center + 0.015
    ax.add_line(Line2D([x_center, x_tick], [y, y], lw=2.5, color=node_colors[i]))
    ax.text(x_text, y + 0.018, date, ha=ha, va="bottom", fontsize=13, color=label_color, weight="bold")
    ax.text(x_text, y - 0.002, label, ha=ha, va="top", fontsize=13, color=label_color)

ax.text(0.5, 0.04, "História da Computação — Parte 1", ha="center", va="center", fontsize=10, color="#b8b8b8")

ax.set_xlim(0,1); ax.set_ylim(0,1); ax.axis("off")
plt.savefig("images/linha-do-tempo-raizes-computacao-vertical.png", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.savefig("images/linha-do-tempo-raizes-computacao-vertical.svg", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.close()

⚙️ Configuração do suanpan

A forma clássica tem 2 contas superiores (5 cada) e 5 inferiores (1 cada) por haste (2:5).
O soroban japonês posterior adota 1:4, otimizado para cálculos rápidos.

1.8 🧵 Tecnologias de registro nas Américas — Quipu andino

🧵 Quipu (Andes, c. 1º milênio d.C.–séc. XVI)

Sistema de cordões com nós em base decimal posicional, usado para censos, tributos e calendários; há pesquisas sobre informação não numérica, ainda em debate.

1.9 ⚙️ Máquina de Anticítera (c. 100 a.C.)

Mecanismo de Anticítera — reconstrução moderna

Descoberta em 1901 num naufrágio perto da ilha de Anticítera, essa engenhoca de bronze é o primeiro computador analógico conhecido.
Calculava posições planetárias e eclipses, unindo astronomia, matemática e mecânica.

🔭 Marco da engenharia antiga

Fragmentos originais no Museu Arqueológico Nacional de Atenas.

Estudos de tomografia e modelagem recentes mostram dials para o ciclo de Saros (223 meses) e reconstruções do trem de engrenagens para Lua/planetas, consolidando o status de computador astronômico capaz de predizer eclipses.

1.9.1 📏 Bastões de Napier (1617)

Inventados por John Napier, criador dos logaritmos, automatizavam multiplicações com varas numeradas.

💡 Impacto matemático

Antepassados da régua de cálculo.
Originais na Biblioteca Nacional da Escócia e em Oxford.

1.9.2 📐 Régua de Cálculo (1632)

Criada por William Oughtred, transformava multiplicações em somas por escalas deslizantes.

🧮 Símbolo da era pré-digital

Base do cálculo analógico moderno.
Modelos no Science Museum (Londres) e no Smithsonian (Washington).

1.9.3 🧠 Máquina de Pascal (1642)

Pascaline — calculadora mecânica de Blaise Pascal

Aos 19 anos, Blaise Pascal construiu a Pascaline, capaz de somar e subtrair automaticamente com engrenagens.

⚙️ Legado histórico

Primeira calculadora comercial funcional.
Exemplares no Musée des Arts et Métiers (Paris) e no Zwinger (Dresden).

Napier (1617) → logaritmos e Bastões (multiplicação por adições); Oughtred (1632) → régua de cálculo, que dominará a engenharia até as calculadoras eletrônicas.

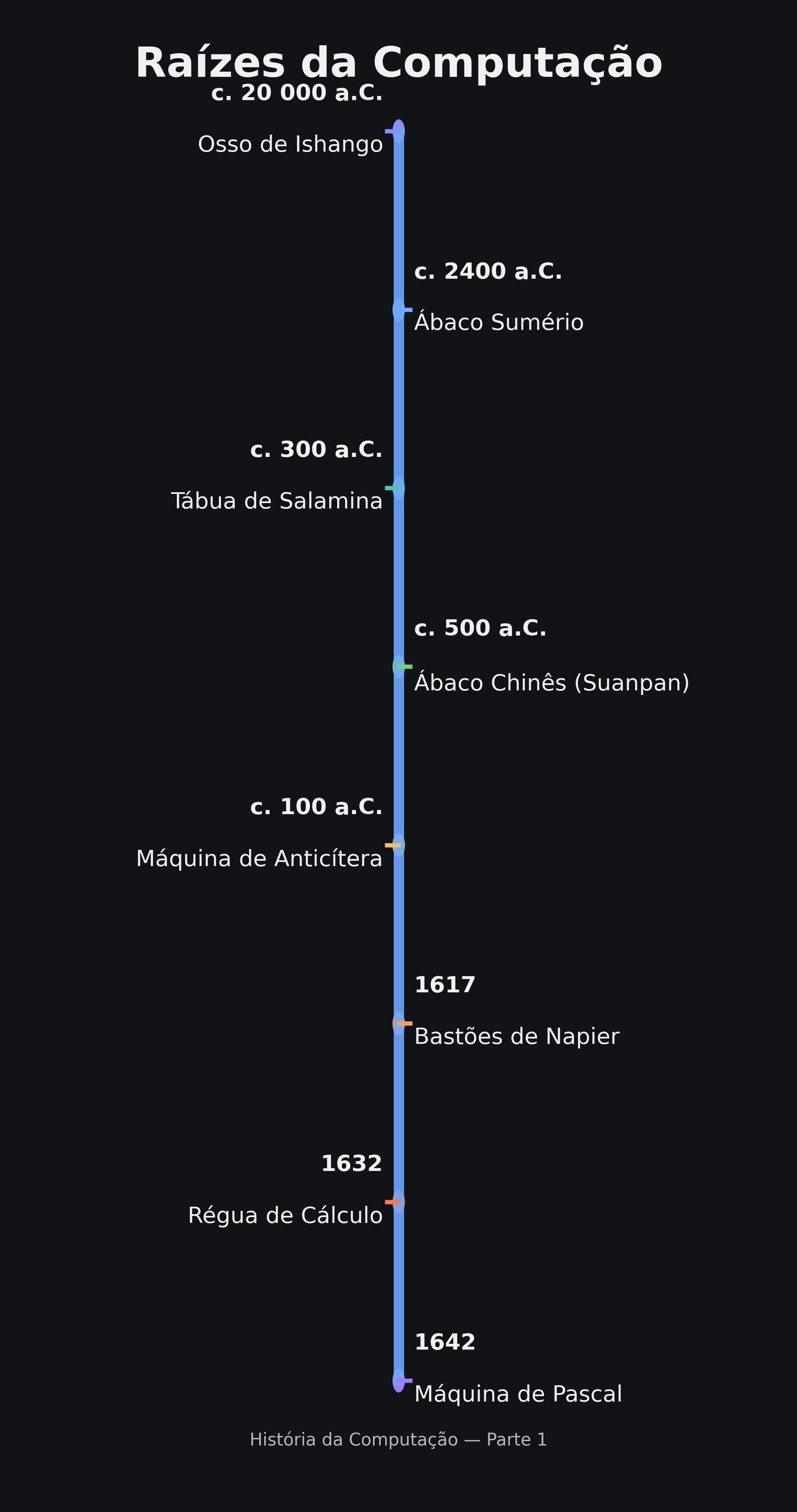
1.10 🕰️ Linha do Tempo — Raízes da Computação

Linha do tempo vertical dos marcos iniciais da computação

Clique para ver o código (Python) — Linha do Tempo Vertical

# Gera: images/linha-do-tempo-raizes-computacao-vertical.png e .svg

import os
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
from matplotlib.lines import Line2D

items = [
    ("Osso de Ishango", "c. 20 000 a.C.", "L"),
    ("Ábaco Sumério", "c. 2400 a.C.", "R"),
    ("Tábua de Salamina", "c. 300 a.C.", "L"),
    ("Ábaco Chinês (Suanpan)", "c. 500 a.C.", "R"),
    ("Máquina de Anticítera", "c. 100 a.C.", "L"),
    ("Bastões de Napier", "1617", "R"),
    ("Régua de Cálculo", "1632", "L"),
    ("Máquina de Pascal", "1642", "R"),
]

os.makedirs("images", exist_ok=True)

bg = "#121316"
timeline_color = "#6ea8fe"
label_color = "#f1f1f1"
node_colors = ["#8b8dfb", "#75a7ff", "#57c0b6", "#6fd17a", "#e8c06f", "#f3a065", "#f17a54", "#9c7cff"]

fig = plt.figure(figsize=(8, 15.5), dpi=300)
ax = plt.gca()
ax.set_facecolor(bg); fig.patch.set_facecolor(bg)

x_center = 0.5
y_top, y_bot = 0.92, 0.08
n = len(items)
ys = [y_top - i * ((y_top - y_bot)/(n-1)) for i in range(n)]

ax.add_line(Line2D([x_center, x_center], [y_bot, y_top], lw=6, color=timeline_color, alpha=0.9, solid_capstyle="round"))
ax.text(0.5, 0.965, "Raízes da Computação", ha="center", va="center", fontsize=24, color=label_color, weight="bold")

for i, ((label, date, side), y) in enumerate(zip(items, ys)):
    ax.add_patch(Circle((x_center, y), 0.008, color=node_colors[i], ec="none"))
    if side == "L":
        x_text = x_center - 0.02; ha = "right"; x_tick = x_center - 0.015
    else:
        x_text = x_center + 0.02; ha = "left";  x_tick = x_center + 0.015
    ax.add_line(Line2D([x_center, x_tick], [y, y], lw=2.5, color=node_colors[i]))
    ax.text(x_text, y + 0.018, date, ha=ha, va="bottom", fontsize=13, color=label_color, weight="bold")
    ax.text(x_text, y - 0.002, label, ha=ha, va="top", fontsize=13, color=label_color)

ax.text(0.5, 0.04, "História da Computação — Parte 1", ha="center", va="center", fontsize=10, color="#b8b8b8")

ax.set_xlim(0,1); ax.set_ylim(0,1); ax.axis("off")
plt.savefig("images/linha-do-tempo-raizes-computacao-vertical.png", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.savefig("images/linha-do-tempo-raizes-computacao-vertical.svg", dpi=300, bbox_inches="tight", facecolor=fig.get_facecolor())
plt.close()

Dica

Síntese. Da abstração pré-histórica ao cálculo mecânico, esses artefatos mostram a jornada humana rumo à mecanização do pensamento lógico.

1.11 🧩 Quiz — As Raízes da Computação

Q1. Qual das opções abaixo descreve melhor o significado histórico do ábaco?

✗Um brinquedo usado em rituais antigos.

✓Um instrumento de cálculo que representou operações mentais em forma física.

✗Um sistema de numeração binária usado pelos gregos.

Q2. Por que a Máquina de Anticítera é considerada um marco?

✗Porque usava eletricidade para calcular.

✗Porque era apenas um calendário solar.

✓Porque utilizava engrenagens mecânicas para prever fenômenos astronômicos — uma forma analógica de computação.

1.12 Referências Rápidas (seleção comentada)

Freeth, T. et al. — estudos de tomografia/modelagem do Mecanismo de Anticítera (dials, ciclos e trem de engrenagens).
Pletser, V.; Huylebrouck, D.; RBINS — leituras e cautelas sobre o Osso de Ishango (regularidade, base 12, controvérsias sobre primos).
Schmandt-Besserat, D. — tokens mesopotâmicos: da contagem à escrita.
Documentação histórica e museológica de suanpan/soroban.
Tábua de Salamina — counting board grega (abax) como elo evolutivo.
Quipu (khipu) — registro decimal posicional andino; usos administrativos e debates sobre informação não numérica.
Napier / Oughtred — logaritmos, Bastões e a régua de cálculo na transição ao cálculo analógico moderno.
Zero e notação indo-arábica — de Brahmagupta a al-Khwārizmī, fundamento dos algoritmos.

📘 Próximo capítulo: 👉 Parte 2 — Era Mecânica

← História da Computação · ← Início · 🔝 Topo

Blog do Marcellini — Explorando a História da Computação com Rigor e Beleza.